|
|
A particle system is the quintessential video game effect used for clouds, fog, mist, smoke, rain, snow, fire, explosions, dust, debris, sparks, magic, spray, splatter, and other phenomenon. They have been around since the early 1980s, William T. Reeves is the inventor, but its most notable debut to the public was when the group that eventually became Pixar (employed by Lucasfilm Ltd. at the time) used a particle system in Star Trek: The Wrath of Khan (1982) for the ‘genesis effect’. It is mystifying that such a classic creative tool is missing from Flash. |
Real time particle systems have been used in games for years and there are loads of knowledgeable resources, as well as source code, available. I stuck close to Pixar’s ‘Physically Based Modeling: Particle System Dynamics’ by Andrew Witkin. If you are looking for some code to get you started there are a number of open source particle systems for Flash, I did not look at the code myself but it looks like Richard Lord took the correct approach in his ‘Flint’ particle system.
This is some of the most optimized Flash code that I have written. On my minimum spec machine (the 8 year old dinosaur aka ‘Computer A’ from my benchmarking series) the system can crank out 2000 simple point particles, my average specification machine has no problem running 5500 point particles with multiple forces (assuming you want to stay at 60fps). Honestly, what can you really do with just points? All I can think of is some cheap sparks and lame rain and snow. The real mark of a high quality particle system is having enough features so you can create convincing effects with few particles, not the volume of particles it can handle. I really wanted to hit the 10,000 particle at 60fps mark, but in order to do so I would have needed to strip out some important functionality. I will talk about some of the special features of this particle system, if you are inspired to write your own, but this article is mainly about optimization tactics for any large system in Flash – using the particle system as an example.
All right, first a couple quick notes of the basics of setting up a Flash particle system. All of my particles exist inside of one bitmap; this is what I was referring to earlier as the correct approach to a Flash particle system. If you want to draw something besides just points in a bitmap, you need to write your own drawing routines and pixel blending code (the bitmap draw method isn’t going to cut it). You really do not have any other alternative. Using a sprite to represent a particle is going to have a very steep initialization cost and bloat the render tree. The other option would be to use the graphics class on one sprite, but there is no render point and you do not want render a vector shape that complex. Rendering is going to take the bulk of the CPU time so you really need to go with the fastest option here, not the easiest. Rendering a point in a bitmap is trivial and you can look up how to alpha blend two colors. By the way, I am incredibly annoyed that bitmaps store color data pre-multiplied but when you get and set values it gives and expects un-multiplied – which means that I have to do a divide every time I blend colors and that flash is internally wasting a bunch of time translating values. I used the Xiaolin Wu algorithm for drawing lines, and wrote my own sphere and light drawing routines.
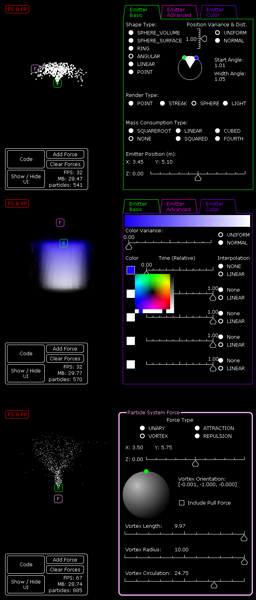 |
The hidden cost of writing a particle system is that you need to write a particle system editor to go with it. There are so many options and settings that having to recompile every time to test will cripple your iteration time, you need real time feedback, think about it as efficiency for the user. It was a significant time sink since I needed to write custom user interface widgets for things like selecting an angle, a 3D orientation selector, and a widget to show color interpolation over time. The most valuable feature is that it generates code for me, so I do not have to copy down settings by hand. It was a significant time sink for me, so keep that in mind if you plan to write your own system. Before we get to optimization strategies there are two advanced features I want to mention briefly: vortex forces and a more sophisticated method for updating particle positions. I had trouble finding sources on vortex forces that were not concerning the vorticity advection process of fluids (which is an n-squared problem and requires inter particle forces or voxels which this system was trying to avoid calculating). |
Once you have your force components properly aligned, creating vortexes, which are typically crafted as cylinders in three-space, it is actually easier than you would think. In order to create the proper vector field, the force in the direction of the center of the vortex (the normal force) needs to equal the force orthogonal to it causing the spin. Those two forces can be scaled relative to the distance to the singularity (the center of the vortex).
|
While you want to increase the forces as you approach the singularity, you will also want to construct some kind of die off to prevent particles uncharacteristically jettisoning themselves from the pull of the vortex. If you were trying to mimic the shape of a vortex similar to natural occurring phenomenon, like a tornado or whirlpool, you would want a force in the direction of the orientation of the cylinder as well, which would increase as you approach the singularity. Accurately moving particles through the vector field is the challenging part. |

|
Moving an object through a complex vector field is a tough concept to wrap your head around if you have not studied calculus. Even tougher, we need to approximate an unknown, and often changing vector field based on our known forces. This involves an area of mathematical relationships called differential equations. Taking an Euler step (the classic position, velocity, and acceleration relationship from introductory physics that assumes constant acceleration) is akin to a linear approximation forward in time based on the forces in the object’s current position. The calculus informed reader will recognize this as approximating a function based on its derivative. If you only need forces that act uniformly on all particles, like gravity, Euler integration is fine. If you are trying to model a space that contains non-uniform forces, you need an approximation with less error. Runge-Kutta of order 4, often abbreviated as RK4, is the common method for calculating positions through these kinds of vector fields. If you computed an Euler step, evaluate the vector field again at the midpoint of the Euler step, and moved forward in time based on the midpoint value – that would be Runge-Kutta of order 2. If you are interested in more information, I would again suggest Pixar’s Physically Based Modeling series ‘Physically Based Modeling: Differential Equation Basics’ by Andrew Witkin and David Baraff.
This first optimization tip is not specific to Flash, but is going to be critical to any large system’s performance. Take the time to analyze your math, often some simple factoring can save a ton of cycles. The other major mathematical optimization comes from revising your project’s math and identifying where you need full accuracy and where it is acceptable to increase performance by using an approximation. As I mentioned before, I wrote all of my own drawing routines for the particle system. Drawing the anti-aliased edge of a circle represents a particularly weighty math problem that I needed to speed up. Finding the area that a pixel overlaps the edge of a circle requires a rather complex integral.
A quick refresher, a circle whose center is at the origin satisfies the equation:
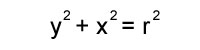
where ‘r’ is the radius of the circle. Rearranged we have:
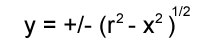
from here on out we will only worry about the positive case. The integral of that function is particularly nasty:

Not only are arcsine and square roots computationally expensive, they also have limited domains. You would have to watch for rounding errors that could result in returning NaN. I desired something faster. I calculated this approximating function:
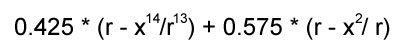
which approximates the curvature of the positive semi-circle with an average relative error margin of 2%; and has a much nicer continuous integral:
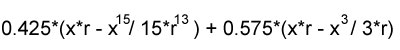
 |
which, with some intelligent factoring, can be coded to execute 10 times faster than the actual integral. I am sure that those of you that favor accuracy are crying out in protest; however, a 2% relative error is well below the tolerance the human eye can detect. Furthermore, pixels are squares; we are using squares to represent a curve, so you might as well discard the notion of being perfectly accurate. Circles have to be large before the approximation function can actually contribute to the shape and you can see artifacts. |
Particles are usually tiny, so tiny that pixels usually cover large portions of the curve and you are comparing relative luminosity of pixels, not overall shape.
The other trick to quickly rendering spheres and light is to use symmetry. You have an object that is symmetric about both the x and y axis (assuming it is centered at the origin). You only need to do the math for one quadrant and you can mirror the results to the other quadrants, which will quarter the work that needs to be done.
Just about every property of my particle system can have a linear or normal distribution variance applied to it (initial speed, mass, lifespan, color, initial position, etc). In the worst case, I need 36 random numbers per birthed particle. That is not crazy expensive, but that cost is completely avoidable. The quality of the random numbers here is not that important, I can cache a bunch of random numbers in advance. I picked a reasonably large prime, 7001, and stored that many random numbers in a circularly linked list, and I just iterate through that list as I need random numbers. Situations like that are rare though, typically you will only find yourself caching the common cases of expensive operations. For example, in my circle drawing code, in the cases where a circle is only rendered in 5 or 9 pixels I stored the values for the min and max pixel coverage and linearly interpolate between them to avoid the integral calculation entirely.
An underlying theme I have discovered with Flash is that you are often better off writing your own code than trusting Adobe’s classes and functions, data structures are no exception. Unless you absolutely need random access, you should switch to a linked list. Reading a property on a class is faster (3 to 6 times faster) than reading a value from an array. Linked lists scale much better if you are storing large objects, and you no longer have to deal with the uncertainty of Adobe’s sort function (they will not tell us what algorithm they use, but it has to be some kind of quick sort since it fails hard when data is nearly sorted). I implemented and benchmarked several different sorts and got the best performance from tiled merge sort, it was always faster than array sort function for particles (12 times faster when particles were nearly sorted – which they usually are since they are sorted every frame). It is annoying to have to write, you can find examples in nearly any beginning programming textbook and on the web, but resulted in huge performance gains when I switched.
Memory issues tend to trip up many Flash programmers; usually we don’t make systems that are that large or complex enough to really worry about memory. We tend to get into a bad habit of casually creating new variables and objects whenever and wherever we need them. Anytime you are creating and destroying a large amount of objects a little efficiency alarm should go off in your head. Memory allocation and de-allocation are expensive processes, and there is no sense in freeing an object from memory when you are going to be creating another one right away. For example, when a particle reaches the end of its lifespan, I store it; when I need to insert new particles in the system, I go to my dead particle list to revive one with new values. I only create new particle when that dead particle list is empty.
Frequently called functions require careful design and attention to memory use, mainly because ActionScript 3 does not have a compiler directive to inline functions. I have several routines called per particle every frame (accumulate forces, calculate new position, figure out your color), and I have a pixel blending function called many times per particle. You could easily create many local variables per particle across several functions, flooding memory with tens of thousands of references to be deleted, which can cause your frame rate to falter when garbage collection cycles. Keep in mind that you are creating a variable for each parameter in the function call, not just when you use the var statement in the function body. With inline not being an option, and my out right refusal to inline by hand, I revised all of the frequently used functions to use permanently declared class variables (and I made them static as well since we don’t have to worry about concurrency since Flash can’t do that either). I looked into the performance difference between local and class variables. A rough rule of thumb is that a local variable would need to be referenced 10 times for reference speed gain out weighs its creation cost, and that value is conceivably higher since we cannot measure the time to remove it from memory. For those not familiar with ActionScript, memory de-allocation is a delayed process that a garbage collector handles (if you assume it equals the creation time the rule would be 20 references for a local variable to pull its weight). If there are minimal references, class variables will be faster than local variables because of the time it takes to create them.
Reusing work done in previous frames can be an extremely powerful optimization tactic. Consider the problem of modeling decaying mass of particles, which you would want to do if you were modeling a chemical reaction like combustion. In sphere and light render modes a particle’s size is determined by its radius, but the relationship between mass and the radius requires a cubed root.
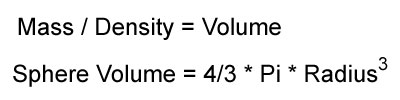
It would be nice to avoid doing such an expensive calculation on every particle. There have been many clever solutions to calculating roots efficiently. The best of which was first implemented for lighting in Quake 3 by Gary Tarolli that leverages the way that numbers are stored as data to get a very close approximation and then applies an iteration of Newton’s Method. Unfortunately, this is Flash and we cannot access the sign, exponent, and mantissa bits of a Number object, but that is no reason to give up. In fact, we can code a more exact approximation that, if all languages were created equal, is less computationally expensive. The trick – we just calculated the cubed root on the last frame (which should be 1/60th of a second ago) and we can use that value as our approximation.
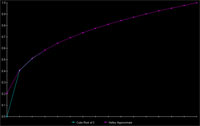 
|
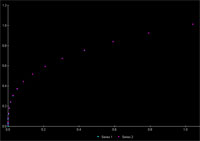
We can do better than Newton’s Method too, upgrading to Halley’s Method allows for cubic convergence at the cost of one more addition and multiplication than Newton’s (which has quadratic convergence). You cannot use this trick all the time, cubed roots are smooth continuous functions, and relatively, do no change much at our frame rate sampling of them (compared to something like the Dirichlet function). Overall, this approximation is just as accurate as taking the expensive power operation. The image to the left is of 15 uniformly dispersed samples of the range 0 to 1: analogous to a particle with initial radius 1, quarter second lifespan, at 60 fps. |
Omitting the case at zero, which is where the particle would be dead anyway, the average relative error is less than one hundredth of a percent. If mass decays at an exponential rate (greater than 1), the approximation is even more accurate since there are more data points as slope increases.
There you have it, my best advice for writing large Flash systems: Used a linked list wherever you can instead of Flash’s Array class, look for opportunities to cache data, if you find yourself doing some complicated math research some approximation alternatives, evaluate your system to see if it can reuse work it did in a past frame, and pay very close attention to your memory use – reusing allocated memory whenever possible. Finally, some general wisdom, do not try to optimize code before you even have something that works and benchmarking is essential – your ‘optimization’ could be slower than the original code or you could be wasting time optimizing code that is not your major bottleneck.
Thanks for reading, and remember, we are all in this together.

|
|
|
Comment by Todd — May 3, 2010 @ 10:47 am
Great article! An extremely thorough examination of the Flash platform and particle systems.
Pingback by Tweets that mention Stephen Calender Programming Blog -- Topsy.com — May 5, 2010 @ 6:00 am
[…] This post was mentioned on Twitter by Snorre Berge. Snorre Berge said: Stephen Calender has a great post on particle systems in Flash: http://bit.ly/cBp3jR […]
Comment by Pascal Sahuc — July 13, 2010 @ 3:03 am
Great article! Thank you for sharing.
One point I am curious about:
“If you want to draw something besides just points in a bitmap, you need to write your own drawing routines and pixel blending code (the bitmap draw method isn’t going to cut it). You really do not have any other alternative.”
I am writing a particle system which renders Sprites whose scale is dynamically and individually varying. Each Sprite contains a single bitmap (which points to the same BitmapData, representing the particle) — note: I am using a Sprite to contain the bitmap particles because it makes scaling via their center easier. All the particle Sprites are children of a single container Sprite, which is rendered via a single draw() call into a bitmap (the composite), whose size matches the stage. I can’t merely copyPixels the particle bitmapData into the bitmap composite, because the scale of each particle is dynamically (and smoothly) changing, at every frame (and no 2 particles have the same scale).
Are you thinking that it would still be faster for me to rely on getPixels32() and setPixels32() to do the scaling, and compositing of my particles in the final bitmap composite?
I hope this makes sense.
Comment by Stephen Calender — August 3, 2010 @ 12:27 am
Hey Pascal,
Yeah, I avoided sprites because it is a tough problem. The bitmap draw method is just as expensive as drawing the graphic normally, I don’t believe there is any optimization if it is the same texture at different scales.
I haven’t done any experimentation with it yet, but I think a super sampling method could be quite fast if you cannot define the shape mathematically. But with how slow bitmap data and Array look ups are you might have to write an optimized data structure for your buffer.
Good Luck!
Comment by Joe Winett — January 14, 2011 @ 3:40 pm
I really appreciate your article. Thanks for taking the time to write and post this!!
Comment by Michael Romis — January 18, 2011 @ 2:32 pm
Wow, little too complicated for me, im just starting to dig through actionscript